شرایط بهینه سازی مسائل برنامه ریزی خطی با ضرایب فازی Optimality conditions for linear programming problems with fuzzy coefficients
Abstract
The optimality conditions for linear programming problems with fuzzy coefficients are derived in this paper. Two solution concepts are proposed by considering the orderings on the set of all fuzzy numbers. The solution concepts proposed in this paper will follow from the similar solution concept, called the nondominated solution, in the multiobjective programming problem. Under these settings, the optimality conditions will be naturally elicited.
Keywords: Fuzzy numbers; Nondominated solutions; (crisp) Fuzzy constraints
چکیده فارسی
شرایط بهینه سازی مسائل برنامه ریزی خطی با ضرایب فازی در این مقاله استنتاج شده است. مفهوم دو راه حل با در نظر گرفتن ترتیب بر روی مجموعه ای از تمام اعداد فازی ارائه شده است. مفاهیم راه حلهای ارائه شده در این مقاله بوسیله مفهوم راه حلی مشابه ، با نام راه حل نامغلوب ، در مسئله برنامه نویسی چند هدفه درک خواهد شد. بر اساس این تنظیمات ، شرایط بهینه سازی به طور طبیعی بدست استنباط خواهد شد.
کلمات کلیدی: اعداد فازی ، راه حل های نامغلوب، محدودیت های فازی(غیردقیق)

مشخصات
توسط: Hsien-Chung Wu مجله: Computers and Mathematics with Applications انتشارات: Elsevier سال انتشار: 2007 میلادی تعداد صفحات متن اصلی: 16 تعداد صفحات متن ترجمه: 36 تاریخ درج: ۱۳۹۵/۸/۲۶ منبع: دیتاسرا

خرید آنلاین فایل ترجمه
عنوان: شرایط بهینه سازی مسائل برنامه ریزی خطی با ضرایب فازی حجم: 358.36 کیلوبایت فرمت فایل: pdf قیمت: 139500 تومان رمز فایل (در صورت نیاز): www.datasara.com نرم افزارهای مورد نیاز: winrar - adobe acrobat - office
تنها با ارسال یک ایمیل وجه خود را دریافت نمایید

دانلود فایل اصلی
عنوان: Optimality conditions for linear programming problems with fuzzy coefficients


1. مقدمه
وقوع فازی در دنیای واقعی در برخی از حوادث غیر مترقبه اجتناب ناپذیر است. بنابراین ، تحمیل فازی بر مشکلات بهینه سازی مرسوم یک موضوع تحقیقاتی جالب می شود. مجموعه ای از مقالات درمورد بهینه سازی فازی توسط استواینسکی و دلگادو و همکاران به چاپ رسیده و جریان اصلی این موضوع را نشان می دهد. لای و هوانگ نیز برآوردی بیشن آفرین در این مورد نشان می دهند. از سوی دیگر ، کتاب به چاپ رسیده توسط استواینسکی و تگم برای مشکلات برنامه نویسی چند هدفه مقایسه ای بین بهینه سازی فازی و بهینه سازی تصادفی ارائه می کند. بلمن و زاده توسط اپراتورهای انبوه ، که ترکیبی از اهداف فازی و فضای تصمیم گیری فازی هستند، گسترش بهینه سازی فازی را القاء می کنند. پس از این انگیزش و القاء ، مقالات بسیاری درمورد مقابله با مشکلات بهینه سازی فازی پدید می آید. برخی از مقالات جالب توسط باکلی، جولین و لوهانجولا و همکاران با استفاده از توزیع احتمال ، هرا و همکاران و و زیمرمان ، با استفاده از محدودیت های فازی شده و توابع هدف ، اینوگوچی و همکاران با استفاده از سنجش های کیفی ، تاناکا و آسای با استفاده از پارامترهای فازی ، و لی و لی [17-19] مجدداً به بررسی مشکل برنامه نویسی پرداختند.
دوگانگی موجود در مشکل برنامه ریزی خطی فازی در مرحله اول توسط رادر و زیمرمان با توجه به تفسیر اقتصادیِ متغیر دوگانه مورد مطالعه قرار گرفت. پس از آن ، بسیاری از نتایج جالب توجه در خصوص دوگانگیِ مسئله برنامه ریزی خطی فازی توسط بکتور و همکاران، لیو و همکاران ، رامیک ، وردگی و وو مورد بررسی قرار گرفتند. در این مقاله ، شرایط بهینه سازی را توسط ضرایب فازی برای مشکلات برنامه ریزی خطی بررسیمی کنیم.
در بخش 2 ، برخی از ویژگی های اصلی و حسابی اعداد فازی را مطرح می نماییم. در بخش 3 ، دو مسئله برنامه ریزی خطی را توسط ضرایب فازی فرمول بندی می کنیم. یکی از مسائل به محدودیت های خطی غیردقیق (متعارف) توجه نموده ، و مسئله دیگر محدودیت های خطی فازی را در نظر می گیرد. دو راه حل برای این دو مسئله ارائه شده است. در بخش 4 ، شرایط بهینه سازی برای این دو مسئله را با معرفی ضریب ها استنباط می کنیم. در نهایت ، در بخش 5 ، سه مثال برای نشان دادن بحث در مورد مسائل برنامه ریزی خطی با ضرایب فازی ارائه شده است.
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
فرض کنیدR (نیاز به دانلود ترجمه) مجموعه ای از تمام اعداد حقیقی است. زیر مجموعه های فازی a ̃ از Rتوسط تابع ξ_a ̃∶R→[0و1] تعریف شده اند که تابع عضویت نامیده می شود. مجموعه ی سطح α از a ̃، که توسط مشخص شده اند، توسط a ̃_α برای تمام αϵ[0و1]تعریف می شوند. مجموعه a ̃_α در سطح 0 ، به صورت مجموعه بسته تعریف شده است ، به عنوان مثال ، (نیاز به دانلود ترجمه) .
تعریف 2.1. ما توسط ، مجموعه ای از تمام زیر مجموعه های فازی a ̃ (نیاز به دانلود ترجمه) از R (نیاز به دانلود ترجمه) را تابع عضویتξ_a ̃ با شرایط زیر نشان می دهیم :
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
(2) ξ_a ̃ (نیاز به دانلود ترجمه) شبه مقعر است ، به عنوان مثال ، (نیاز به دانلود ترجمه) برای همه (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) می باشد؛
(3) ξ_a ̃ (نیاز به دانلود ترجمه) ، به عنوان مثال ، (نیاز به دانلود ترجمه) زیر مجموعه بسته ای از U (نیاز به دانلود ترجمه) برای هر (نیاز به دانلود ترجمه) است؛
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
جزء a ̃ در (نیاز به دانلود ترجمه) یک عدد فازی نامیده می شود.
اکنون فرض کنید که (نیاز به دانلود ترجمه) است. به گفته زاده ، مجموعه a ̃_α در سطح( a) ̃ (نیاز به دانلود ترجمه) زیر مجموعه ای محدب از R برای هر (نیاز به دانلود ترجمه) در وضعیت (2) می باشد. با ترکیب این واقعیت با شرایط (3) و (4) ، مجموعه a ̃_α در سطح0 زیر مجموعه ای بهم پیوسته و محدب از R برای همه می باشد. ، یعنی a ̃_α در یک بازه ی بسته R (نیاز به دانلود ترجمه) برای هر می باشد. بنابراین آن را بصورت (نیاز به دانلود ترجمه) می نویسیم.
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
تذکر 2.1. فرض کنید ( a) ̃ یک عدد فازی باشد. بنابراین اگر ( a) ̃نامنفی باشد و آنگاه و برای همه (نیاز به دانلود ترجمه) است، و اگر ( a) ̃مثبت باشد و آنگاه و (نیاز به دانلود ترجمه) برای همه (نیاز به دانلود ترجمه) است . می توانیم نتایج مشابهی را برای اعداد فازی غیرمثبت و منفی داشته باشیم.
فرض کنید (نیاز به دانلود ترجمه) ، عملیاتی دودویی برای ⊕ یا ⊗بین دو عدد فازی ( a) ̃و ( b) ̃است. تابع عضویت به صورت زیر تعریف می شوند:
با استفاده از اصل گسترش زاده ، در عملیات (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) متناظر با و (نیاز به دانلود ترجمه) می باشد. پس می توانیم نتایج زیر را بگیریم.
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
(1) و
(2) و
قضیه ای به شرح زیر بسیار مفید برای بحث در مورد شرایط بهینه سازی است .
قضیه 2.2. فرض کنید ( a) ̃ یک عدد فازی نامنفی و ( b) ̃ یک عدد فازی نامثبت باشد. اگر باشد، آنگاه برای همه ، می باشد.
اثبات : از قضیه 2.1 (2) ، بلافاصله داریم که است ، پس
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
برای همه است. بنابراین ، نیاز داریم که نشان دهیم که برای همه است . موارد زیر را در نظر می گیریم.
(1) فرض کنید که (نیاز به دانلود ترجمه) است. آنگاه بوده و در نتیجه (نیاز به دانلود ترجمه) می باشد. بنابراین (نیاز به دانلود ترجمه) است، یعنی ، (نیاز به دانلود ترجمه) است.
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
(3) فرض کنید که (نیاز به دانلود ترجمه) است. سپس (نیاز به دانلود ترجمه) است. چون ، است و ما توسط گزینه (1) می دانیم (نیاز به دانلود ترجمه) است. بنابراین( a) ̃ نامنفی است، (نیاز به دانلود ترجمه) نشان می دهد که است. اثباتمان کامل شد.
می گوییم که ( a) ̃در صورتی یک عدد غیردقیق با ارزش m که تابع عضویت آن باشد:
همچنین از نماد (نیاز به دانلود ترجمه) برای نشان دادن عدد غیردقیق با ارزش m استفاده می کنیم. آسان است که نشان دهیم (نیاز به دانلود ترجمه) برای همه (نیاز به دانلود ترجمه) است. فرض کنید که عدد حقیقی m را می توان به عنوان یک عدد غیردقیق (نیاز به دانلود ترجمه) در نظر گرفت.
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
فرض کنید (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) دو فاصله بسته باشند. می نویسیم (نیاز به دانلود ترجمه) است اگر و تنها اگر (نیاز به دانلود ترجمه) ، باشد و (نیاز به دانلود ترجمه) است اگر و تنها اگر به شرح زیر باشد :
فرض کنید a ̃و b ̃دو عدد فازی هستند. سپس و دو فاصله بسته در Rبرای همه (نیاز به دانلود ترجمه) می باشند. می نویسیم اگر و تنها اگر برای همه (نیاز به دانلود ترجمه) است یا برای همه معادل است.به آسانی مشاهده می شود که یک ترتیب جزئی در (نیاز به دانلود ترجمه) می باشد.
برای راحتی ، ما توسط ~ 0 عدد غیردقیق (نیاز به دانلود ترجمه) با را بصورت می نویسیم. اینک دو مسئله برنامه ریزی خطی زیرا را با ضرایب فازی در نظر می گیریم:
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
که در آن یک عدد غیردقیق با ارزش برای (نیاز به دانلود ترجمه) می باشد. مسئله (FLP1) محدودیت های غیردقیق (متعارف) ، و مسئله (FLP2) محدودیت های فازی را در نظر می گیرد. برای ارائه مناسب ، می نویسیم:
نیاز به تفسیر معنای کمینه سازی مسائل (نیاز به دانلود ترجمه) (FLP1) و (FLP2)داریم. از آنجا که (نیاز به دانلود ترجمه) یک ترتیب جزئی بر روی (نیاز به دانلود ترجمه) است نه ترتیب کلی، ممکن است ما به دنبال مفهومی مشابه باشیم که (راه حل نامغلوب ) در مورد مسئله برنامه نویسی چند هدفه برای تفسیر معنی کمینه سازی مسائل (FLP1) و ( FLP2) بکار رفته است.
دو نوع راه حل نامغلوب را در نظر خواهیم گرفت. می نویسیم (نیاز به دانلود ترجمه) است اگر و تنها اگر (نیاز به دانلود ترجمه) برای همه (نیاز به دانلود ترجمه) باشد و (نیاز به دانلود ترجمه) وجود داشته باشد به طوری که (نیاز به دانلود ترجمه) باشد ، به عنوان مثال:
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
بنابراین ، می بینیم که به معنای و (نیاز به دانلود ترجمه) می باشد. ازسوی دیگر ، می نویسیم (نیاز به دانلود ترجمه) است اگر و تنها اگر برای همه (نیاز به دانلود ترجمه) باشد. یعنی (2) برای ایفای (نیاز به دانلود ترجمه) می باشد.
تعریف 3.1 . فرض کنید x* یک راه حل عملی برای مسئله (FLP1)است. می گویند که x* در صورتی راه حل نامغلوب نوع 1 مسئله (FLP1)است( نسبت به راه حل نامغلوب نوع2) که هیچ راه حل عملی (نیاز به دانلود ترجمه) وجود نداشته باشد به طوری که (نیاز به دانلود ترجمه) باشد. راه حل های نامغلوب نوع 1 و 2 را می توان به طور مشابه برای مسئله (FLP2) در نظر گرفت.
در ادامه ، ما به دنبال ارائه شرایط بهینه سازی برای راه حل نامغلوب مسئله های (FLP1) و (FLP2) می رویم.
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
به منظور استنباط شرایط بهینه سازی مسئله های (FLP1) و (FLP2)، نیاز به یادآوری شرایط کاروش - کوهن - تاکر برای مسئله برنامه ریزی غیر خطی داریم. فرض کنید ، ارزش واقعی توابع تعریف شده در (نیاز به دانلود ترجمه) است. سپس مسئله برنامه ریزی غیر خطی (متعارف) زیر را در نظر می گیریم :
فرض کنیم که توابع محدود (نیاز به دانلود ترجمه) در (نیاز به دانلود ترجمه) برای هر (نیاز به دانلود ترجمه) محدب هستند. آنگاه شرایط بهینه سازی شناخته خوب شده کاروش - کوهن - تاکر برای مسئله(NLP) (به عنوان مثال ، به هورست و همکاران یا بازارا و همکاران نگاه کنید) بشرح ذیل می باشد.
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
آنگاه x* راه حلی بهینه برای مسئله (NLP) است.
اکنون ما در موقعیتی استنباط شرایط بهینه سازی برای مسئله های (FLP1) و (FLP2) هستیم.
4.1 . محدودیت های غیردقیق (متداول)
اینک مسئله (FLP1) را با محدودیتهای غیردقیق در نظر بگیرید. ما نمادهای زیر را اتخاذ می نماییم:
که در آن (نیاز به دانلود ترجمه) و برای همه هستند . همچنین می بینیم (نیاز به دانلود ترجمه) برای همه (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) است. همچنین توسط (نیاز به دانلود ترجمه) بردار واحد در (نیاز به دانلود ترجمه) را برای نشان می دهیم ، به عنوان مثال ، مولفه kthاز برابر با 1 است و سایر مولفه های صفر هستند.
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
(1)
(2) (نیاز به دانلود ترجمه) برای همه (نیاز به دانلود ترجمه) ، همه (نیاز به دانلود ترجمه) ، (نیاز به دانلود ترجمه) می باشد ، که در آن است،
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
اثبات : به دنبال اثبات این نتیجه تناقض می رویم. فرض کنید که شرایط (1) و (2) اجرا شده اند و x* یک راه حل نامغلوب نوع 1 نیست. آنگاه یک راه حل عملی برای این مسئله (نیاز به دانلود ترجمه) وجود دارد ،به طوری که (نیاز به دانلود ترجمه) است ، به عنوان مثال ، ازمورد (2)، داریم:
(3)
برای برخی (نیاز به دانلود ترجمه) است. از آنجا که برای i = 1, . . . , n و برای همه (نیاز به دانلود ترجمه) و همه i = 1, . . . , nاست ، با استفاده از قضیه 2.1، داریم:
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
همچنین داریم:
(5)
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
(6)
سپس می بینیم که
(7) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه)
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
(8) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه)
پس (نیاز به دانلود ترجمه) و است .علاوه بر این ، از (5) و (7) ، داریم:
(9) (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه)
مسئله بهینه سازی محدود شده زیر را در نظر می گیریم:
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
با استفاده از قضیه 4.1 ، می بینیم که شرایط (1) و (2) فوق شرایط KKT برای مسئله (P1) هستند. بنابراین ، نتیجه گیری می کنیم که x* راه حلی بهینه شده از مسئله d (P1) می باشد ، یعنی ، ، که در تضاد با مورد (8) است. این اثبات کامل شد.
تذکر 4.1. توابع ارزش واقعی مثبت ، (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) ، و توابع ارزش واقعی نامنفی μj و (نیاز به دانلود ترجمه) برای j = 1, . . . ,m, و k = 1, . . . , n را می توان به شرح زیر ایجاد نمود. برای هر گونه (نیاز به دانلود ترجمه) ثابت ، اگر برای j = 1, . . . ,m, و k = 1, . . . , n اعداد واقعی مثبت (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) ، و اعداد واقعی نامنفی (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) وجود داشته باشد، شرایط زیر را اعمال می گردد:
سپس می توانیم توابع با ارزش واقعی مثبت ، (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) را برای همه (نیاز به دانلود ترجمه) ، و توابع با ارزش واقعی نامنفی (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) را برای همه (نیاز به دانلود ترجمه) و همه j = 1, . . . ,m, و k = 1, . . . , n تعریف نماییم. بنابراین ، در صورتی که شرایط فوق (الف) و (ب) برای (نیاز به دانلود ترجمه) ،اعمال گردد، آنگاه x* راه حل نامغلوب نوع 1 مسئله (FLP1) توسط قضیه 4.2 می باشد.
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
آنگاه x* راه حل نامغلوب نوع 2 برای مسئله(FLP1) می باشد.
اثبات : برای اثبات به دنبال رد نتایج می رویم. فرض کنید که حالات (1) و (2) اعمال گردیدند و x* راه حل نامغلوب نوع 2 نیست. آنگاه راه حلی عملی برای (نیاز به دانلود ترجمه) وجود دارد به طوری که (نیاز به دانلود ترجمه) ، برای تمام (نیاز به دانلود ترجمه) اعمال می گردد. می توانیم برای (نیاز به دانلود ترجمه) در شرایط (1) و (2) ، تابعی با ارزش حقیقی را تعریف کنیم :
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
سپس می بینیم که:
(11) (نیاز به دانلود ترجمه)
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
مابقی اثبات مشابه قضیه 4.2 می باشد.
اکنون بدون در نظر گرفتن به دنبال ارائه شرایط بهینه سازی برای راه حل نامغلوب نوع 2 می باشیم.
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
تذکر 4.2. فرض کنید بتواند یک عدد فازی باشد و تابع عضویت آن به شدت در فاصله زمانی افزایش یابد و در فاصله (نیاز به دانلود ترجمه) به شدت کاهش یابد. آنگاه ، و (نیاز به دانلود ترجمه) با توجه به واقعیت یکنواختی و متغیر α در [0،1] توابع پیوسته می باشند. این امر نشان می دهد که عدد فازی متعارف است.
فرض کنید (نیاز به دانلود ترجمه) یک تابع برداری تعریف شده روی فاصله بسته باشد به طوری که هر یک از مولفه های (نیاز به دانلود ترجمه) (نیاز به دانلود ترجمه) بر روی [a, b] شود. آنگاه انتگرال ریمان f در [a, b] برای هر یک از مولفه های انتگرال ریمان (نیاز به دانلود ترجمه) [a, b] تعریف می شود. بطور دقیقتر ، داریم:
اینک با در نظر گرفتن انتگرال ریمان در موقعیت ارائه نوع دیگری از شرایط بهینه سازی هستیم.
قضیه 4.4. فرض کنید که ضرایب فازی برای i = 1, . . . , n در تابع هدف با ارزش فازی (نیاز به دانلود ترجمه) اعداد فازی متعارف تصور می شود. فرض کنید راه حل عملی مسئله(FLP1) است. در صورتی که اعداد با ارزش واقعی مثبت (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) ارزش واقعی نامنفی (نیاز به دانلود ترجمه) μj و (نیاز به دانلود ترجمه) برایj = 1, . . . ,m و k = 1, . . . , n به گونه ای وجود داشته باشد که شرایط زیر اعمال گردد : (نیاز به دانلود ترجمه)
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
آنگاه x*راه حل نامغلوب نوع 2 برای مسئله(FLP1) می باشد.
اثبات : برای هر x ثابت ، نظر به اینکه و بر روی [0،1] پیوسته بوده و با توجه به متغیر α ، انتگرال ریمان در [0،1] (نیاز به دانلود ترجمه) خواهد بود. بنابراین ، می توانیم یک تابع حقیقی را به شرح زیر تعریف نماییم:
برای هر α ثابت، نظر به اینکه (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) توابع خطی هستند ، به طور مداوم ، توسط R قضیهرادین [قضیه 9.42]مشتقپذیر هستند و داریم:
(14)
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
برای همه (نیاز به دانلود ترجمه) با توجه به (نیاز به دانلود ترجمه) و این امر اعمال می گردد. با گرفتن انتگرال α در [0،1] و با استفاده از (13) ، را به دست می آوریم. اینک مسئله بهینه سازی محدود شده (P1) را که در قضیه 4.2 اثبات شده را در نظر می گیریم. فرمول (14) را در حالت (1) و (2) این قضیه بکار می بریم و دو حالت زیر به دست می آوریم :
مابقی اثبات مشابه قضیه 4.2 می باشد.
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
آنگاه قضیه 4.4 اگر حالت (1) با حالات جدید زیر جایگزین شود، باز هم صادق می باشد:
اینک به دنبال ارائه شرایط بهینه سازی مسئله (FLP1) به شکل ارزش فازی می رویم. ما را می نویسیم. فرض کنید x ، بردار n در است. آنتگاه بردار غیردقیق به صورت (نیاز به دانلود ترجمه) تعریف می شود. فرض کنید (نیاز به دانلود ترجمه) n بردار در است . میگوییم که a علامتی یکسان دارد اگر و تنها اگر به طور همزمان برای همهi = 1, . . . , n ، باشد، یا برای همهi = 1, . . . , n به طور همزمان باشد(به عنوان مثال ، مولفه های بردار a علامتی یکسان دارند). یا بطور معادل، a علامتی یکسان دارد اگر و تنها اگر (نیاز به دانلود ترجمه) یا باشد.
قضیه 4.5. فرض کنید x*راه حلی عملی برای مسئله(FLP1) و است. فرض می کنیم که هر بردار (نیاز به دانلود ترجمه) دارای علامت یکسانی برای j = 1, . . . ,m ،k = 1, . . . , n است. اگر اعداد فازی نامنفی (نیاز به دانلود ترجمه) برایj = 1, . . . ,m و k = 1, . . . , n وجود داشته باشند به طوری که حالات زیر اعمال شود،
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
اثبات : فرض کنیم می که حالات (1) و (2) اعمال شده اند. فرض می کنیم و (نیاز به دانلود ترجمه) مجموعه شاخص های تعریف شده توسط فرمول زیر باشند؛
آنگاه
مولفه i ام فرمول در حالت (1) بصورت زیر نشان داده می شود:
(15)
که در آن است، اگر و (نیاز به دانلود ترجمه)
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
برای همه است ، که همچنین ، با اضافه کردن آنها به هم ایجاب می شود،
(16)
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
برای همه و همه j = 1, . . . ,m است و
برای همه و همه است k = 1, . . . , n ، که ، با اضافه کردن آنها را با هم این مفهوم را میرسانند ،
(17)
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
(18)
برای همه و همه k = 1, . . . , n است. در حال حاضر مسئله بهینه سازی محدود شده (P1)را مانند اثبات قضیه 4.2 در نظر می گیریم. با توجه به رابطه (16) - (18) و (9) ، دو حالت جدید به دست می آوریم :
الف) (توجه داشته باشید که (16) برای اعمال می گردد) ؛
ب) (نیاز به دانلود ترجمه) برای همه j = 1, . . . ,m و همه k = 1, . . . , n (توجه داشته باشید که (17) و (18) برای همه اعمال شده است).
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
4.2 محدودیت های فازی
اینک به دنبال استنباط شرایط بهینه سازی مسئله (FLP2) با محدودیت های فازی می رویم. یادآوری می کنیم که محدودیت های فازی برای (نیاز به دانلود ترجمه) j = 1, . . . ,m به صورت زیر ارائه شده اند:
با استفاده از قضیه 2.1 ، برای (نیاز به دانلود ترجمه) داریم:
که در آن
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
آنگاه (نیاز به دانلود ترجمه) و است. اینک در موقعیتی استنباط شرایط بهینه سازی مسئله (FLP2) قرار داریم.
قضیه 4.6. فرض کنید x*راه حل عملی برای مسئله (FLP2) است.
(الف)در صورت وجود ، توابع (نیاز به دانلود ترجمه) و (نیاز به دانلود ترجمه) با ارزش واقعی مثبت در [0،1] ، و ، توابع μj و (نیاز به دانلود ترجمه) ارزش واقعی نامنفی برای j = 1, . . . ,m و همه k = 1, . . . , n (نیاز به دانلود ترجمه) در [0،1] به طوری که شرایط زیر اعمال گردد :
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
(ب) در صورت وجود ، توابع (نیاز به دانلود ترجمه) وبا (نیاز به دانلود ترجمه) ارزش واقعی مثبت در [0،1] ، و ، توابع μj و (نیاز به دانلود ترجمه) با ارزش واقعی نامنفی برایj = 1, . . . ,m و همه k = 1, . . . , n (نیاز به دانلود ترجمه) در [0،1] به طوری که شرایط زیر اعمال گردد :
آنگاه x* راه حل نامغلوب نوع 1 برای مسئله (FLP2) می باشد.
اثبات( الف): برای اثبات به دنبال رد نتایج می رویم. فرض کنید که حالات (1) و (2) اعمال گردیدند و x* یک راه حل نامغلوب نوع 1 نیست. آنگاه راه حلی عملی برای (نیاز به دانلود ترجمه) وجود دارد به طوری که (نیاز به دانلود ترجمه) است ، به عنوان مثال ، در فرمول (3) حدود است (نیاز به دانلود ترجمه) . اینک ارزش واقعی تابع f در فرمول (6) یا در فرمول (7) را تعریف می کنیم و مسئله بهینه سازی محدود شده زیرا در نظر می گیریم:
جهت مشاهده متن کامل، فایل ترجمه را دانلود نمایید.
با استفاده از قضیه 4.1 ، می بینیم که x* با رعایت شرایط فوق (1) و (2) به عنوان شرایط KKT راه حلی بهینه برای مسئله(P2) است، یعنی (نیاز به دانلود ترجمه) ، که در تضاد با (8) است.
(ب) ما اینک مسئله بهینه سازی محدود شده زیرا در نظر می گیریم:
سپس می بینیم که اگر x* راه حلی عملی برای مسئله (FLP2) باشد، آنگاه x* راه حل عملی برای مسئله (P2) نیز است. استدلال های مشابه فوق نیز می توانند مورد استفاده قرار گیرند. این امر اثبات را کامل می کند.
قضیه 4.7. فرض کنید x*راه حلی عملی برای مسئله (FLP2)است .
Optimality conditions for linear programming problems with fuzzy coefficients
شرایط بهینه سازی مسائل برنامه ریزی خطی با ضرایب فازی
ISI
Paper
Papers
Article
Articles
مقاله ISI
اعداد فازی
دانلود ISI
ترجمه مقاله
ISI کامپیوتر
دریافت مقاله
مقاله انگلیسی
Fuzzy numbers
Persian Paper
خرید ترجمه ISI
Persian Article
ترجمه مقاله ISI
دانلود مقاله ISI
مقاله رایگان ISI
دانلود ترجمه ISI
خرید ترجمه مقاله
دانلود مقاله جدید
دریافت مقالات ISI
مقالات رایگان ISI
راه حل های نامغلوب
مقاله ISI کامپیوتر
فروش ترجمه انگلیسی
خرید ترجمه انگلیسی
مقاله انگلیسی جدید
مقاله ISI با ترجمه
دانلود مقاله انگیسی
دانلود ISI کامپیوتر
ترجمه مقاله انگلیسی
مقالات معتبر انگلیسی
ترجمه مقالات انگلیسی
ترجمه مقاله کامپیوتر
دریافت مقاله انگلیسی
دانلود مقاله جدید ISI
دریافت مقاله کامپیوتر
Nondominated solutions
مقاله انگلیسی کامپیوتر
مقاله انگلیسی با ترجمه
دانلود رایگان مقاله ISI
خرید ترجمه ISI کامپیوتر
Translate English Paper
دانلود مقالات رایگان ISI
ترجمه مقاله ISI کامپیوتر
دانلود مقاله انگلیسی جدید
(crisp) Fuzzy constraints
دانلود ترجمه ISI کامپیوتر
خرید ترجمه مقاله کامپیوتر
Translate English Article
مقاله رایگان ISI کامپیوتر
محدودیت های فازی(غیردقیق)
دریافت مقاله انگلیسی جدید
دانلود مقاله ISI کامپیوتر
دانلود مقاله ISI با ترجمه
ترجمه مقالات معتبر انگلیسی
Translate Paper in English
دریافت مقالات ISI کامپیوتر
دانلود مقاله جدید کامپیوتر
مقالات رایگان ISI کامپیوتر
مقاله ISI با ترجمه کامپیوتر
دانلود مقاله انگلیسی رایگان
دانلود رایگان مقاله انگلیسی
دانلود مقاله انگلیسی رایگان
دریافت مقاله انگلیسی رایگان
مقاله انگلیسی جدید کامپیوتر
فروش ترجمه انگلیسی کامپیوتر
خرید ترجمه انگلیسی کامپیوتر
ترجمه مقاله انگلیسی کامپیوتر
Translate Article in English
دانلود مقاله انگیسی کامپیوتر
دریافت مقاله انگلیسی کامپیوتر
دانلود مقاله انگلیسی با ترجمه
دریافت مقاله انگلیسی با ترجمه
ترجمه مقالات انگلیسی کامپیوتر
مقالات معتبر انگلیسی کامپیوتر
دانلود مقاله جدید ISI کامپیوتر
Translation of Paper in English
مقاله انگلیسی با ترجمه کامپیوتر
دانلود رایگان مقاله ISI کامپیوتر
دانلود مقالات رایگان ISI کامپیوتر
Translation of Article in English
دانلود مقاله ISI با ترجمه کامپیوتر
دانلود مقاله انگلیسی جدید کامپیوتر
دریافت مقاله انگلیسی جدید کامپیوتر
ترجمه مقالات معتبر انگلیسی کامپیوتر
دانلود مقاله انگلیسی رایگان کامپیوتر
دریافت مقاله انگلیسی رایگان کامپیوتر
دانلود رایگان مقاله انگلیسی کامپیوتر
دانلود مقاله انگلیسی رایگان کامپیوتر
دریافت مقاله انگلیسی با ترجمه کامپیوتر
دانلود مقاله انگلیسی با ترجمه کامپیوتر
به سوی پایگاه داده چندگانه (اشتراکی) انعطاف پذیر و مستقل
.png)
.png)
Abstract The success of cloud computing as a platform for deploying webapplications has led to a deluge of applications characterized by small data footprints with unpredictable access patterns. A scalable multitenant ... [ ادامه مطلب ]
انتشارات: ACM
 قیمت: 119500 تومان
قیمت: 119500 تومان
 قیمت: 119500 تومان
قیمت: 119500 تومان

رویکردی در ارتباط با معماری خط تولید سرویسگرا
.png)
.png)
Abstract Service-Oriented Architecture (SOA) has appeared as an emergent approach for developing distributed applications as a set of self-contained and business-aligned services. SOA aids solving integration and interoperability problems and provides ... [ ادامه مطلب ]
انتشارات: ACM
 قیمت: 119500 تومان
قیمت: 119500 تومان
 قیمت: 119500 تومان
قیمت: 119500 تومان

ظرفیت شبکه های بی سیم
.png)
.png)
Abstract When n identical randomly located nodes, each capable of transmitting at W bits per second and using a fixed range, form a wireless network, the throughput (formula) obtainable by each ... [ ادامه مطلب ]
انتشارات: ACM
 قیمت: 139500 تومان
قیمت: 139500 تومان
 قیمت: 139500 تومان
قیمت: 139500 تومان

سیستم های صف بندی زمان گسسته با تعطیلی های انحصاری مارکوفب
.png)
.png)
Abstract In this contribution we investigate discrete-time queueing systems with vacations. A framework is constructed that allows for studying numerous different vacation systems, including a.o. classical vacation systems like the exhaustive ... [ ادامه مطلب ]
انتشارات: ACM
 قیمت: 129500 تومان
قیمت: 129500 تومان
 قیمت: 129500 تومان
قیمت: 129500 تومان

عوامل تعیینکننده در انتخاب نرمافزار وبمحور معنایی در قالب یک سرویس:
چارچوبی یکپارچه در شرایط خرید الکترونیکی و برنامه ریزی منابع سرمایه ای
.png)
.png)
Abstract The ever increasing Internet bandwidth and the fast changing needs of businesses for effectiveness with the partners in the procurement chain and is leading organizations to adopt information systems infrastructures ... [ ادامه مطلب ]
انتشارات: ACM
 قیمت: 119500 تومان
قیمت: 119500 تومان
 قیمت: 119500 تومان
قیمت: 119500 تومان

طراحی و تحلیل یک مدل وقفه (تعطیلی) برای سیستم صف بندی دو فازه با خدمات ورودی
.png)
.png)
Abstract This paper mainly deals with a two phase service queueing model with gated service vacation. In this gated service vacation model, only those customers who are present in the queue ... [ ادامه مطلب ]
انتشارات: ACM
 قیمت: 129500 تومان
قیمت: 129500 تومان
 قیمت: 129500 تومان
قیمت: 129500 تومان

به اشتراک گذاری طیف مشارکتی بین شبکه های تلفن همراه و اد هاک
.png)
.png)
Abstract Spectrum sharing between cellular and ad-hoc networks is studied in this work. Weak signals and strong interferences at the cell-edge area usually cause severe performance degradation. To improve the cell-edge ... [ ادامه مطلب ]
انتشارات: ACM
 قیمت: 139500 تومان
قیمت: 139500 تومان
 قیمت: 139500 تومان
قیمت: 139500 تومان

مقایسه پروتکل های مسیر یابی تک مسیره در مقابل پروتکل های مسیر یابی چندگانه برای انتقال تصویر در شبکه های حسگر بی سیم چند رسانه ای
.png)
.png)
Abstract Wireless multimedia sensor network (WMSN) applications require strong multimedia communication competence. Therefore, in WMSN applications, it is necessary to use specific mechanisms in order to handle multimedia communication challenges and ... [ ادامه مطلب ]
انتشارات: ACM
 قیمت: 129500 تومان
قیمت: 129500 تومان
 قیمت: 129500 تومان
قیمت: 129500 تومان

هوش کسب و کار به روش محاسبه ابری
.png)
.png)
Abstract Business Intelligence (BI) deals with integrated approaches to management support. Currently, there are constraints to BI adoption and a new era of analytic data management for business intelligence these constraints ... [ ادامه مطلب ]
انتشارات: ACM
 قیمت: 119500 تومان
قیمت: 119500 تومان
 قیمت: 119500 تومان
قیمت: 119500 تومان

مدل احتمال جدید برای ضمانت کردن مشکل مسیر بحرانی با الگوریتم اکتشافی
.png)
.png)
Abstract In order to obtain an adequate description of risk aversion for insuring critical path problem, this paper develops a new class of two-stage minimum risk problems. The first-stage objective function ... [ ادامه مطلب ]
انتشارات: ACM
 قیمت: 129500 تومان
قیمت: 129500 تومان
 قیمت: 129500 تومان
قیمت: 129500 تومان

دستورالعمل طراحی و محاسبه سیستم روشنایی
.png)
.png)
مجموعه دستورالعمل های ارائه شده در دیتاسرا شامل ضوابط و مراحل تحلیل و طراحی سازه های گوناگون صنعتی و بر اساس الزامات مندرج در آیین نامه های معتبر داخلی و ... [ ادامه مطلب ]
 قیمت: 119500 تومان
مشخصات کلی:
قیمت: 119500 تومان
مشخصات کلی:
صفحات متن اصلی: 30
گروه:
دستورالعمل طراحی
 قیمت: 119500 تومان
قیمت: 119500 تومان
صفحات متن اصلی: 30
گروه: دستورالعمل طراحی

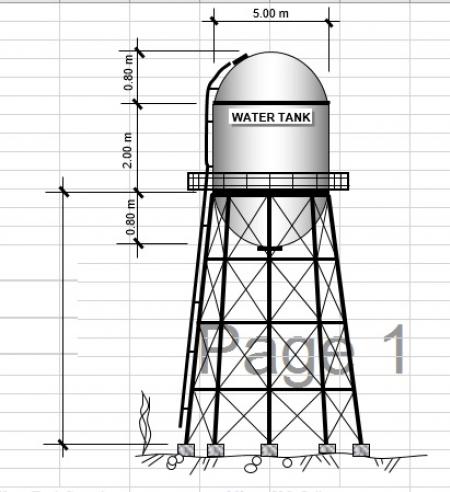
فایل اکسل طراحی مخزن فلزی هوایی بر اساس آیین نامه AISC با در نظر گرفتن نیروی باد و زلرله
.png)
.png)
فایل پیش رو اکسل طراحی مخزن فلزی هوایی می باشد که بر اساس آیین نامه AISC و با در نظر گرفتن نیروی باد و زلرله محاسبات را انجام داده و ... [ ادامه مطلب ]
 قیمت: 79500 تومان
مشخصات کلی:
قیمت: 79500 تومان
مشخصات کلی:
گروه:
دستورالعمل طراحی
 قیمت: 79500 تومان
قیمت: 79500 تومان
گروه: دستورالعمل طراحی

فایل اکسل تحلیل اتصال برشی دارای خروج از مرکزیت برای گروه پیچ
.png)
.png)
این برنامه ظرفیت برشی اتصال پیچ و مهره ای دارای خروج از مرکزیت برای گروه پیچ را محاسبه می کند، ابزاری مناسب برای طراحی صفحات gusset و اتصالات پیچ و ... [ ادامه مطلب ]
 قیمت: 79500 تومان
مشخصات کلی:
قیمت: 79500 تومان
مشخصات کلی:
گروه:
دستورالعمل طراحی
 قیمت: 79500 تومان
قیمت: 79500 تومان
گروه: دستورالعمل طراحی

فایل اکسل طراحی روسازی آسفالتی بر مبنای آیین نامه آشتو و استفاده از آزمایش ظرفیت باربری کالیفرنیا
.png)
.png)
فایل پیش رو اکسل طراحی روسازی آسفالتی بر مبنای آیین نامه آشتو می باشد که با استفاده از نتایج آزمایش ظرفیت باربری کالیفرنیا CBR اطلاعات ورودی را تحلیل و نتایج را ... [ ادامه مطلب ]
 قیمت: 79500 تومان
مشخصات کلی:
قیمت: 79500 تومان
مشخصات کلی:
گروه:
دستورالعمل طراحی
 قیمت: 79500 تومان
قیمت: 79500 تومان
گروه: دستورالعمل طراحی

دستورالعمل طراحی ابعاد و سازه شالوده های عمیق (شمع ها و پایه های عمیق) در خشکی
.png)
.png)
مجموعه دستورالعمل های ارائه شده در دیتاسرا شامل ضوابط و مراحل تحلیل و طراحی سازه های گوناگون صنعتی و بر اساس الزامات مندرج در آیین نامه های معتبر داخلی و ... [ ادامه مطلب ]
 قیمت: 119500 تومان
مشخصات کلی:
قیمت: 119500 تومان
مشخصات کلی:
صفحات متن اصلی: 27
گروه:
دستورالعمل طراحی
 قیمت: 119500 تومان
قیمت: 119500 تومان
صفحات متن اصلی: 27
گروه: دستورالعمل طراحی

تحلیل غیرخطی و مدل سازی عددی تیر بتن مسلح تقویت شده با FRP توسط Finite Element Method
.png)
.png)
"پایان نامه مهندسی عمران مقطع کارشناسی ارشد - گرایش سازه" تحلیل غیرخطی و مدل سازی عددی تیر بتن مسلح تقویت شده با FRP توسط Finite Element Method مشخصات کلی: شامل فایلهای word و ... [ ادامه مطلب ]
 قیمت: 129500 تومان
مشخصات کلی:
قیمت: 129500 تومان
مشخصات کلی:
گروه:
دستورالعمل طراحی
 قیمت: 129500 تومان
قیمت: 129500 تومان
گروه: دستورالعمل طراحی

بررسی پارامترهای هندسی مهاربند زانویی
.png)
.png)
"پروژه دانشجویی مهندسی عمران" بررسی پارامترهای هندسی مهاربند زانویی مشخصات کلی: شامل فایلهای word و pdf بالغ بر 146 صفحه (4 فصل) فهرست مطالب فصل اول 1-1- مقدمه 1-2- شکل پذیری سازه ها 1-3- مفصل و لنگر پلاستیک 1-4- منحنی ... [ ادامه مطلب ]
 قیمت: 129500 تومان
مشخصات کلی:
قیمت: 129500 تومان
مشخصات کلی:
گروه:
دستورالعمل طراحی
 قیمت: 129500 تومان
قیمت: 129500 تومان
گروه: دستورالعمل طراحی

تحلیل و طراحی سیستم گرمایشی ساختمان مسکونی با استفاده از ذخیره کننده های حرارتی PCM
.png)
.png)
"پایان نامه مهندسی مکانیک مقطع کارشناسی ارشد - گرایش تبدیل انرژی" تحلیل و طراحی سیستم گرمایشی ساختمان مسکونی با استفاده از ذخیره کننده های حرارتی PCM تهیه شده بصورت کاملا انحصاری توسط ... [ ادامه مطلب ]
 قیمت: 449000 تومان
مشخصات کلی:
قیمت: 449000 تومان
مشخصات کلی:
گروه:
دستورالعمل طراحی
 قیمت: 449000 تومان
قیمت: 449000 تومان
گروه: دستورالعمل طراحی

شناسایی و رتبه بندی دلایل انحراف از هزینه پیش بینی شده و ارائه راهکارهای کاهش آن: مطالعه موردی پروژه های "پتروشیمی الف"
.png)
.png)
"پایان نامه مهندسی عمران مقطع کارشناسی ارشد - گرایش مهندسی و مدیریت ساخت" شناسایی و رتبه بندی دلایل انحراف از هزینه پیش بینی شده و ارائه راهکارهای کاهش آن: مطالعه ... [ ادامه مطلب ]
 قیمت: 259500 تومان
مشخصات کلی:
قیمت: 259500 تومان
مشخصات کلی:
گروه:
دستورالعمل طراحی
 قیمت: 259500 تومان
قیمت: 259500 تومان
گروه: دستورالعمل طراحی

مکانیک شکست (Fracture Mechanics)
.png)
.png)
مقدمه : یکی از عمده ترین مسائلی که انسان از زمان ساختن سادهترین ابزارها با آن مواجه بوده است پدیده شکست در اجسام میباشد و درواقع برای استفاده از مواد ... [ ادامه مطلب ]
 قیمت: 99500 تومان
مشخصات کلی:
قیمت: 99500 تومان
مشخصات کلی:
گروه:
دستورالعمل طراحی
 قیمت: 99500 تومان
قیمت: 99500 تومان
گروه: دستورالعمل طراحی



.png)